planer_truss.m
function planer_truss clear all; close all; init_params2(); global np;global ne;global nb;global nf; global nodes;global elems; global cnsts;global loads; % load exp1; load exp2; draw_truss(); axis equal; eks = {}; K = zeros(np*2); F = zeros(np*2,1); u = zeros(np*2,1); computeLocalStiffnessMatrix(); computeTotalStiffnessMatrix(); loadBoundaryCondition(); loadForce(); % u=K\F; u = gaussian_elimination(K,F); fprintf('[computed displacement]\n'); u draw_displaced_truss(); function computeLocalStiffnessMatrix() for idx=1:ne n1=elems(idx,2); n2=elems(idx,3); n1x=nodes(n1,2); n1y=nodes(n1,3); n2x=nodes(n2,2); n2y=nodes(n2,3); z = (n2x-n1x) + (n2y-n1y) * i; theta = angle(z); deg = theta*180/pi; c = cos(theta); s = sin(theta); l = abs(z); A = elems(idx,4); E = elems(idx,5); k = A*E/l; ek = k * [ c^2 c*s -c^2 -c*s c*s s^2 -c*s -s^2 -c^2 -c*s c^2 c*s -c*s -s^2 c*s s^2 ]; eks = [eks; {n1,n2, ek}]; end end function computeTotalStiffnessMatrix() for idx=1:ne it = double(cell2mat(eks(idx,1))); jt = double(cell2mat(eks(idx,2))); ek = cell2mat(eks(idx,3)); ll = [2*it-1,2*it,2*jt-1,2*jt]; for ie=1:4 for je=1:4 K(ll(ie),ll(je)) = K(ll(ie),ll(je)) + ek(ie,je); end end end end function loadBoundaryCondition() count = size(cnsts,1); for i=1:count idx = cnsts(i,1); xidx = 2*idx; yidx = 2*idx-1; isXConstrained = cnsts(i,2); isYConstrained = cnsts(i,3); if(isXConstrained==1) K(xidx,:) = 0; K(:,xidx) = 0; K(xidx,xidx) = 1; end if(isYConstrained==1) K(yidx,:) = 0; K(:,yidx) = 0; K(yidx,yidx) = 1; end end end function loadForce() count = size(loads,1); for idx=1:count fidx = loads(idx,1); F(2*fidx-1) = loads(idx,2); F(2*fidx) = loads(idx,3); fx_origin = nodes(fidx,2); fy_origin = nodes(fidx,3); fx_dist = fx_origin+loads(idx,2); fy_dist = fy_origin+loads(idx,3); drawArrow([fx_origin,fx_dist],[fy_origin,fy_dist]); end end function draw_truss() count = size(elems,1); for i=1:count n1=elems(i,2); n2=elems(i,3); n1x=nodes(n1,2); n1y=nodes(n1,3); n2x=nodes(n2,2); n2y=nodes(n2,3); plot([n1x,n2x],[n1y,n2y],'b-'); hold on; end end function draw_displaced_truss() count = size(elems,1); for i=1:count n1=elems(i,2); n2=elems(i,3); n1x=nodes(n1,2)+u(2*n1-1); n1y=nodes(n1,3)+u(2*n1); n2x=nodes(n2,2)+u(2*n2-1); n2y=nodes(n2,3)+u(2*n2); plot([n1x,n2x],[n1y,n2y],'r--'); hold on; end end function drawArrow(x,y) quiver( x(1),y(1),x(2)-x(1),y(2)-y(1),0 ); end end
init_params2.m
function init_params2 np=10; ne=16; nb=2; nf=1; nodes = [ 1,0,0 2,1,0 3,2,0 4,3.5,0 5,4.0,0 6,3.5,2 7,2,2 8,2,1 9,1,2 10,0,2 ]; elems = [ 1,1,2,1,1 2,2,3,1,1 3,3,4,1,1 4,4,5,1,1 5,5,6,1,1 6,6,4,1,1 7,4,7,1,1 8,7,8,1,1 9,8,3,1,1 10,9,8,1,1 11,2,8,1,1 12,2,9,1,1 13,1,9,1,1 14,6,7,1,1 15,7,9,1,1 16,9,10,1,1 ]; cnsts = [ 1,1,1 10,1,1 ]; loads = [ 5,0.0,-0.005 ]; save exp2; end
gaussian_elimination.m
function ans = gaussian_elimination(A,b) % A = [2 6 28; % 3 4 27; % 4 14 60]; % % b = [34 66 68]'; % A = [1 -2 3 % 3 1 -5 % -2 6 -9] % b = [1 -4 -2]' ans = solveLinearEquation(A,b); function x = solveLinearEquation(A,b) [A,b] = forward_elimination(A,b); x = backward_substitution(A,b); function [A,b]=forward_elimination(A,b) n=length(A); for i=1:n pivot = A(i,i); for j=1:n A(i,j) = A(i,j)/pivot; end b(i) = b(i) / pivot; for k=i+1:n pivot2 = A(k,i); for j=i:n A(k,j) = A(k,j) - A(i,j)*pivot2; end b(k) = b(k) - b(i)*pivot2; end end end function x=backward_substitution(A,b) n=length(A); x(n) = b(n); for i=n-1:-1:1 res = 0; for j=i+1:n res = res + A(i,j) * x(j); end x(i) = b(i) - res; end end end end
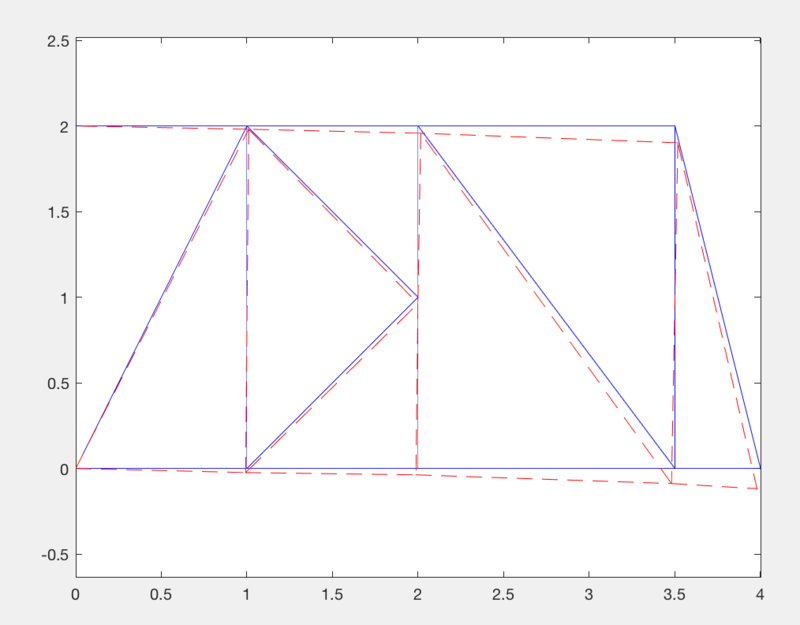
計算結果
[computed displacement]
u =
Columns 1 through 6
0 0 -0.0075 -0.023975 -0.0125 -0.037296
Columns 7 through 12
-0.02 -0.088078 -0.020625 -0.1184 0.016875 -0.098078
Columns 13 through 18
0.015 -0.042296 -0.00125 -0.037296 0.01 -0.018975
Columns 19 through 20
0 0